Inventor教學影片 << Previous Next >> W10-W18

W7

原本是c語言，可以改用y:\tcc\tcc.exe -run 進行類解譯, 但是必須把檔名以.c為結尾

#include <stdio.h>
  
int main() {
    printf("Hello, world!\n");
    return 0;
}

/* Runge Kutta for a set of first order differential equations */
  
#include <stdio.h>
#include <math.h>
  
#define N 2 /* number of first order equations */
#define dist 0.1 /* stepsize in t*/
#define MAX 30.0 /* max for t */
  
FILE *output; /* internal filename */
FILE *output1; /* internal filename */
// 利用 pipe 呼叫 gnuplot 繪圖
FILE *pipe;
  
void runge4(double x, double y[], double step); /* Runge-Kutta function */
double f(double x, double y[], int i); /* function for derivatives */
  
void main(){
  
  double t, y[N];
  int j;
  
  output=fopen("osc.dat", "w"); /* external filename */
  output1=fopen("osc1.dat", "w"); /* external filename */
  
  y[0]=2.0; /* initial position */
  y[1]=1.0; /* initial velocity */
  
  //fprintf(output, "0\t%f\n", y[0]);
  
  for (j=1; j*dist<=MAX ;j++) /* time loop */{
  
    t=j*dist;
    runge4(t, y, dist);
    fprintf(output, "%f\t%f\n", t, y[0]);
    fprintf(output1, "%f\t%f\n", t, y[1]);
  }
  
  fclose(output);
  fclose(output1);
  
  pipe = popen("gnuplot -persist","w");
  //fprintf(pipe,"set term png enhanced font \"v:/fireflysung.ttf\" 18 \n");
  fprintf(pipe,"set term png enhanced font \"y:/wqy-microhei.ttc\" 18 \n");
  //fprintf(pipe,"set yrange [68:70]\n");
  fprintf(pipe,"set output \"test.png\"\n");
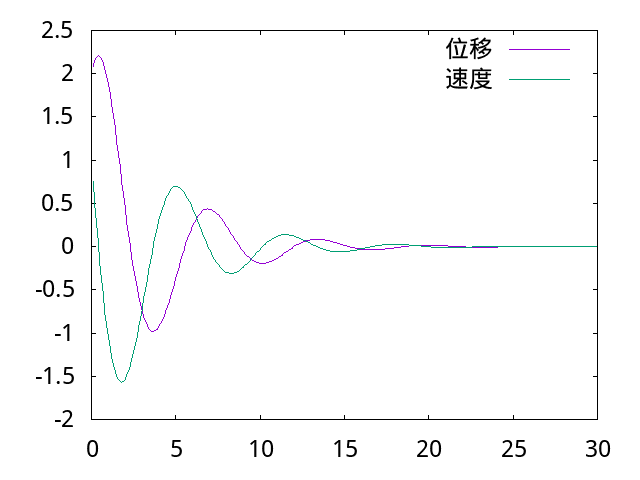
  fprintf(pipe, "plot \"osc.dat\" title \"位移\" with lines, \"osc1.dat\" title \"速度\" with lines\n");
  fprintf(pipe,"quit\n");
 
  fprintf(pipe,"quit\n");
  pclose(pipe);
}
  
void runge4(double x, double y[], double step){
  
  double h=step/2.0, /* the midpoint */
  t1[N], t2[N], t3[N], /* temporary storage arrays */
  k1[N], k2[N], k3[N],k4[N]; /* for Runge-Kutta */
  int i;
  
  for (i=0;i<N;i++){
  
    t1[i]=y[i]+0.5*(k1[i]=step*f(x,y,i));
  }
  
  for (i=0;i<N;i++){
  
    t2[i]=y[i]+0.5*(k2[i]=step*f(x+h, t1, i));
  }
  
  for (i=0;i<N;i++){
  
    t3[i]=y[i]+ (k3[i]=step*f(x+h, t2, i));
  }
  
  for (i=0;i<N;i++){
  
    k4[i]= step*f(x+step, t3, i);
  }
  
  for (i=0;i<N;i++){
  
    y[i]+=(k1[i]+2*k2[i]+2*k3[i]+k4[i])/6.0;
  }
}
  
double f(double x, double y[], int i){
  
  if (i==0)
    x=y[1]; /* derivative of first equation */
  if (i==1)
    x=-y[0]-0.5*y[1];
  return x;
}

上述所解的狀態方程式:

質量為 1kg 物理, 以 k=1 彈簧與 b=0.5 阻尼器連接在固定牆壁, 起始拉開 1m, 速度為０時放開, 求放開質量後的運動模擬.

$x (t)$ 表示質量拉開水平方向設為正向 x, 且為時間 t 的函式

起始條件: $x (0) =2 .0 ，$ $\dot{x} (0) =1$

以下利用程式定義解題:

$x = y [0]$

$\dot{x} = y [1]$

$\ddot{x} = - y [0] - 0.5 * y [1]$

並產生數值運算結果:

Inventor教學影片 << Previous Next >> W10-W18